APLICACIONES DE GRAFOS
- 25 may 2016
- 4 Min. de lectura
OBJETIVO
Mostrar la aplicación de la teoría de grafos dentro de los márgenes de diseño en la vida real y los diferentes programas utilizados, ya sea en estructuras de comunicación, y dirigidos a la ejecución de programas.
GENERALIDADES


Gracias a la teoría de grafos se pueden resolver diversos problemas como por ejemplo la síntesis de circuitos secuenciales, contadores o sistemas de apertura. Se utiliza para diferentes áreas por ejemplo, Dibujo computacional, en todas las áreas de Ingeniería. Los grafos se utilizan también para modelar trayectos como el de una línea de autobús a través de las calles de una ciudad, en el que podemos obtener caminos óptimos para el trayecto aplicando diversos algoritmos como puede ser el algoritmo de Floyd. Para la administración de proyectos, utilizamos técnicas como PERT en las que se modelan los mismos utilizando grafos y optimizando los tiempos para concretar los mismos. La teoría de grafos también ha servido de inspiración para las ciencias sociales, en especial para desarrollar un concepto no metafórico de red social que sustituye los nodos por los actores sociales y verifica la posición, centralidad e importancia de cada actor dentro de la red.
REPRESENTACION DE GRAFOS EN PROGRAMAS
Representacion mediante matrices : La forma mas facil de guardar la informacion de los nodos es mediante la utilización de un vector que indexe los nodos , de manera que los arcos entre los nodos se pueden ver como relaciones entre los indices. Esta relacion entre indices se puede guardar en una matriz, que llamaremos de adyacencia .

REPRESENTACION DE UN GRAFO DIRIGIDO
Representación mediante listas.
En las listas de adyacencia lo que haremos sera guardar por cada nodo, ademas de la informacion que pueda contener el propio nodo , una lista dinamica con lo nodos a los que se pueda accerder desde el . La informacion de los nodos se puede guardear en una vector al igual que antes , o en otra lista dinamica

Representación de un grafo dirigido.
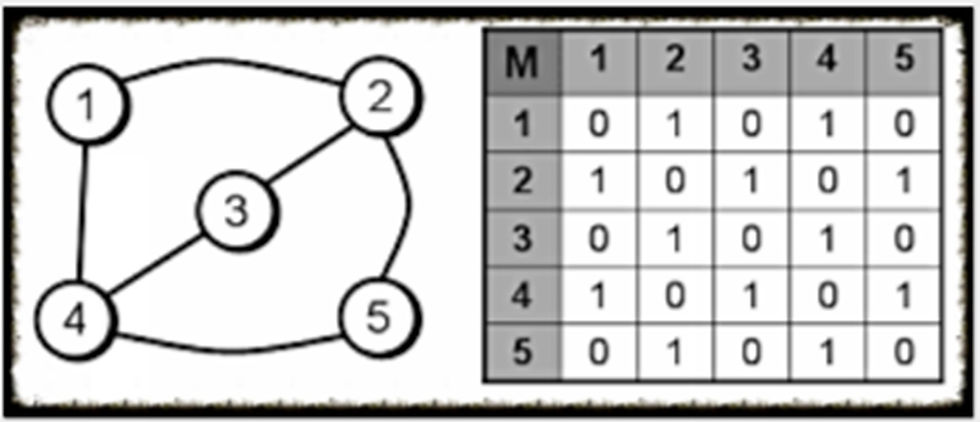
Para la representación de la matriz se utilizara la siguiente condición:
1- Cuando ingresamos 1 , es debido a que el vértice i esta conectado con el vértice j, de lo contrario pondremos 0 en donde el vértice i no esta conectado con e vértice J .
MODELOS CON GRAFOS
Los grafos se emplean en una variedad de modelos en diferentes areas, en este caso se mostrara algunos modelos empleados en el area computacional.

GRAFOS DE LLAMADAS
Los grafos se pueden utilizar para representar las llamadas telefónicas hechas en una red, por ejemplo en una red telefónica de larga distancia. En particular, puede usarse un multígrafo dirigido para representar llamadas: cada vértice representa un número de teléfono y cada arista representa una llamada. La arista que representa una llamada sale del número del teléfono desde el que se hace la llamada y llega al número de que lo recibe. En la siguiente figura que ilustraremos, se muestra un pequeño grafo de llamadas telefónicas que representa siete números de teléfono. Este grafo muestra, por ejemplo, que se han hecho cinco llamadas telefónicas desde el 732-555-1234 al 732-555-4444 a ninguno de los otros seis números, salvo al 732-555-0011. Cuando solo nos importa si ha habido o no alguna llamada entre dos números, empleamos un grafo no dirigido tal que una arista conecta dos números de teléfono si se ha hecho alguna llamada en dichos números. Esta versión del grafo de llamadas la mostraremos a continuación:

Grafo de la Red
La red de Internet se puede representar mediante un grafo dirigido en el que cada página Web está representada por un vértice y en el que una arista comienza en la página a y termina en la página b si hay un enlace en la página a que conduce a la página b.

Como cada segundo se crean páginas Web nuevas y otras desaparecen, hay más de mil millones de vértices y decenas de miles de millones de aristas. Hay muchas personas estudiando las propiedades del grafo de la red para entender mejor la naturaleza de la red de Internet.
GRAFOS DE PRECEDENCIA Y PROCESAMIENTO CONCURRENTE
Los programas informáticos, más que todo para los Sistemas Operativos, pueden ejecutarse más rápidamente si ciertas sentencias se ejecutan simultáneamente. Es importante no ejecutar sentencias que requieran el resultado de sentencias no ejecutadas. La dependencia de sentencias con respecto a sentencias previas se puede representar por medio de un grafo dirigido. Cada sentencia se representa por un vértice, y hay una arista de un vértice a un segundo si la sentencia representada por el segundo vértice no puede ejecutarse hasta la sentencia representada por el primero se ha ejecutado. A este tipo de grafo se le llama grafo de precedencia. Por ejemplo, el grafo nos dice que la sentencia S₅ no se puede ejecutar hasta que se ejecute S₁, S₂, y S₄.

S1 a:= 0; S2 b:= 1 ;S3 c:= a+1 (necesita que s1 se ejecute para que s3 se ejecute); S4 d:= b+a (necesita que s1 y s2 se ejecute para que s4 se ejecute); S5 e:= d+1 (necesita que s4 se ejecute para que s5 se ejecute); S6 f:= d+c (necesita que s4 y s3 se ejecuten para que s6 se ejecute)
VIDEO
https://www.youtube.com/watch?v=V90L9IkVPso
BIBLIOGRAFÍA
http://javeriana.edu.co/biblos/tesis/ciencias/tesis341.pdf
http://mdunidad6.blogspot.com.co/2011/12/teoria-de-grafos.html http://docencia.udea.edu.co/regionalizacion/teoriaderedes/informaci%F3n/C1_RepresentacionMatrices.pdf http://www.dma.fi.upm.es/personal/gregorio/grafos/

















































Comentarios